SEMANA 29--DIVISIÓN DE POLINOMIOS.
SEPTIEMBRE 1
Competencias a desarrollar:
Los estudiantes serán capaces de dividir polinomios , de memorizar y resolver algoritmos de productos notables.
Bibliografía:
División de polinomios. video:
P r o c e d i m i e n t o :
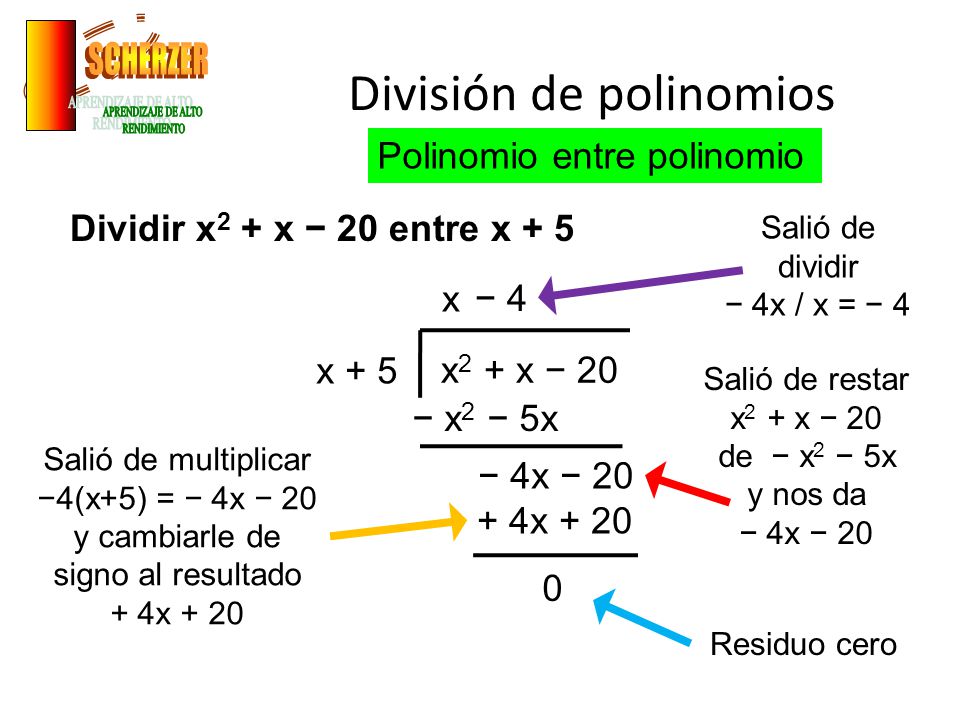
1. Se ordenan los dos polinomios respecto a una misma letra
2. Se divide el primer término del dividendo entre el primer término del divisor, éste será el primer término del cociente
3. El primer término del cociente se multiplica por cada uno de los términos del divisor y el producto obtenido se resta del dividendo, para lo cual se cambia el signo, y escribiendo cada término debajo de su semejante
4. Se divide el primer término del resto entre el primer término del divisor, éste será el segundo término del cociente
5. El segundo término del cociente se multiplica por cada uno de los términos del divisor y el producto se resta del resto que quedó en el dividendo, cambiando los signos y escribiendo cada término debajo de su semejante
6. Se divide el primer término del segundo resto entre el primero del divisor y se efectúan las operaciones anteriores ...
7. Se continúa así sucesivamente hasta que el residuo sea cero.
Por definición, sabemos que un polinomio está formado por la suma o resta de varios monomios.
Un polinomio se puede dividir por un monomio o por otro polinomio.
La operación es muy similar a la división tradicional de números, donde hay un divisor, un dividendo, un cociente y un resto.
Dividir un polinomio se ve más complejo por la inclusión de términos algebraicos que tienen letras y números.
Por ello, para explicar la división de polinomios desarrollaremos un ejercicio práctico:
Vamos a dividir el polinomio
(6x 5 + x 4 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)
Primero, ordenamos tanto el dividendo como el divisor de mayor a menor según sus grados, y completamos el grado que falte:
(6x 5 + x 4 + 0x 3 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)
En el dividendo agregamos 0x 3 ya que ese grado faltaba.
Ahora, el polinomio, que es el dividendo, lo colocamos a la izquierda, y el divisor lo ponemos enmarcado a la derecha:
Dividimos el primer monomio del dividendo (+6x 5 ) entre el primer monomio del divisor (+2x 2 ).
+6x 5 : +2x 2 = +3x 3
Este resultado (+3x 3 ) lo ponemos debajo de la caja y lo multiplicamos por cada término del polinomio divisor y el resultado lo vamos restando en el polinomio dividendo:
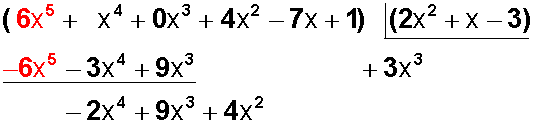
Aquí debemos tener cuidado: al multiplicar +3x 3 , primero por +2x 2 ; luego por + x y luego por -3, hay que tener en cuenta la regla de los signos, y el resultado que pongamos abajo en el dividendo debe llevar signo contrario al obtenido.
Bajamos el monomio siguiente (+4x 2 ) y continuamos:
Ahora dividimos -2x 4 : +2x 2 = -x 2
Y este resultado lo agregamos al cociente y lo multiplicamos por +2x 2 , luego por +x y luego por -3:
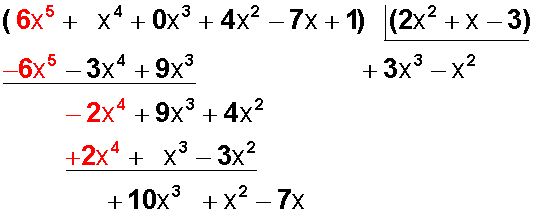
Bajamos e monomio siguiente (-7x),
y ahora dividimos +10x 3 : + 2x 2 = + 5x
Y +5 x lo agregamos al cociente, lo multiplicamos por +2x 2 , luego por+ x y luego por -3:
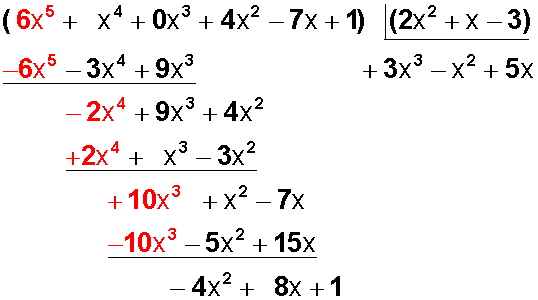
Bajamos el último monomio (+1),
y ahora dividimos -4x 2 : +2x 2 =-2
-2 lo agregamos al cociente y repetimos la operación anterior:
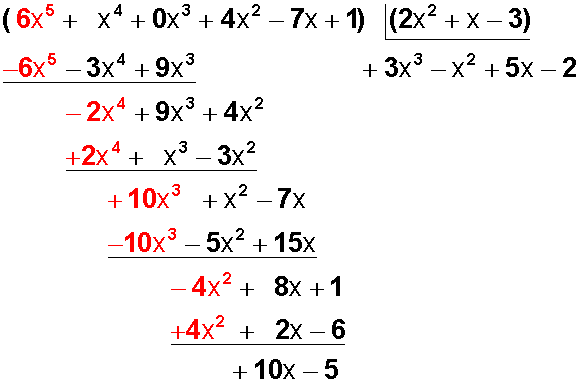
Ahora no queda nada más por bajar en el dividendo y si el grado del resto (+10x) es menor que el grado del divisor (2x 2 ), hemos terminado la división.
Cociente o resultado: +3x 3 – x 2 + 5x -2
Resto: +10x -5
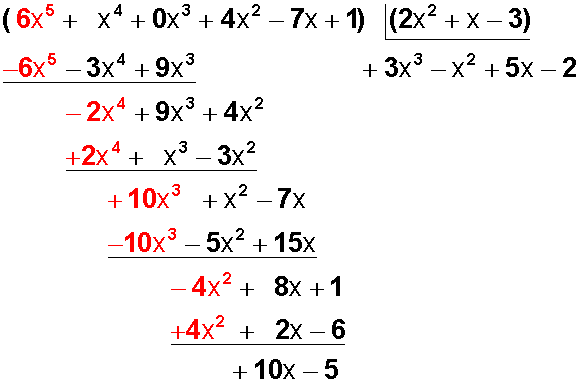
Ejemplos:
a) clic ( con fraccionarios)
b) clic
c) clic
En este link pueden encontrar más videos de división de polinomios con fraccionarios.


Comentarios
Publicar un comentario